本文目录导读:
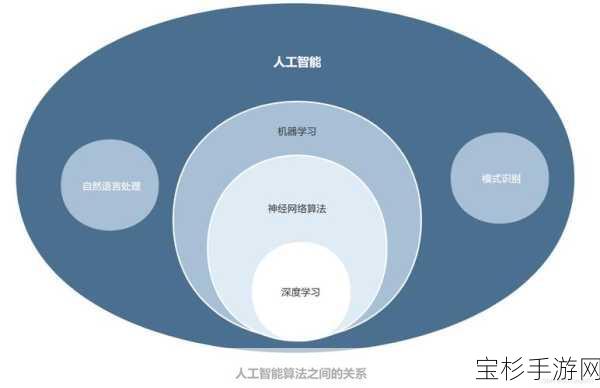
在人工智能的浪潮中,机器学习作为其核心驱动力之一,正以前所未有的速度改变着我们的生活和工作方式,从自动驾驶汽车到智能推荐系统,从医疗诊断到金融风控,机器学习的身影无处不在,在这背后,是一系列复杂而精妙的数学原理支撑着这些智能算法的运行与优化,本文旨在深入探讨机器学习中不得不知的数学基础,帮助读者更好地理解这一领域,并为进一步的学习和实践打下坚实的基础。
一、线性代数:构建数据空间的基石
线性代数是机器学习中最基础也是最重要的数学工具之一,它研究向量、矩阵及其运算,为数据的表示、变换和分析提供了强有力的数学框架。
向量与矩阵:在机器学习中,数据通常以向量的形式表示,而矩阵则是处理这些向量的主要工具,向量的点积、叉积等操作在特征提取、距离计算等方面有着广泛应用;矩阵的乘法、转置、逆等操作则是实现线性变换、求解线性方程组的基础。
线性变换与特征值分解:线性变换是数据降维、特征提取的重要手段,通过特征值分解(如PCA主成分分析),我们可以找到数据的主要成分,实现数据的压缩和去噪,奇异值分解(SVD)在推荐系统中也扮演着重要角色,它能够帮助我们从用户-物品评分矩阵中提取潜在特征。
二、概率论与统计学:量化不确定性的艺术
概率论与统计学为机器学习提供了处理不确定性数据的方法,是构建预测模型、评估模型性能的关键。
概率分布与随机变量:在机器学习中,数据往往具有随机性,因此我们需要通过概率分布来描述数据的特性,常见的概率分布包括正态分布、二项分布、泊松分布等,它们在不同的应用场景中发挥着重要作用。
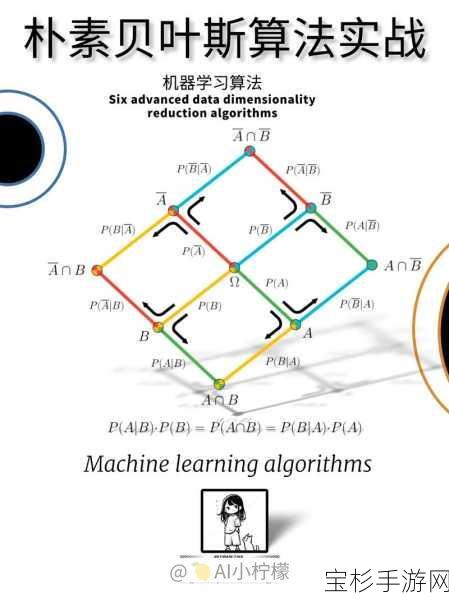
贝叶斯定理:贝叶斯定理是机器学习中的核心思想之一,它提供了一种根据先验知识和观测数据更新信念的方法,在分类、回归等任务中,贝叶斯方法能够提供直观的解释和稳健的性能。
假设检验与置信区间:在统计学中,假设检验用于判断样本数据是否支持某个假设;置信区间则给出了参数估计的可靠性范围,这些工具在模型评估、参数调优等方面至关重要。
三、微积分与优化:求解最优解的利器
微积分与优化理论是机器学习算法实现高效、准确预测的关键,它们帮助我们找到损失函数的最小值,从而优化模型参数。
导数、偏导数与梯度:在机器学习中,损失函数通常是一个关于模型参数的多元函数,通过计算导数、偏导数和梯度,我们可以了解损失函数随参数变化的趋势,进而指导参数的更新方向。
梯度下降法及其变体:梯度下降法是一种常用的优化算法,它通过迭代更新参数来最小化损失函数,为了加速收敛、避免陷入局部最优解,人们提出了多种变体,如随机梯度下降(SGD)、动量法、Adam等。
拉格朗日乘数法与凸优化:在处理带有约束条件的优化问题时,拉格朗日乘数法提供了一种有效的求解方法,凸优化理论在机器学习中也具有重要地位,因为它保证了全局最优解的存在性和唯一性。
四、信息论与编码:理解数据信息的桥梁
信息论研究信息的度量、传输和处理,为机器学习中的特征选择、数据压缩等任务提供了理论基础。
熵与互信息:熵是衡量随机变量不确定性的度量,而互信息则用于量化两个随机变量之间的相关性,在特征选择中,我们可以利用互信息来评估特征与目标变量之间的相关性,从而筛选出最有价值的特征。
数据压缩与编码:在信息论中,数据压缩旨在减少数据的存储和传输成本,通过霍夫曼编码、算术编码等算法,我们可以实现高效的数据压缩,这对于处理大规模数据集具有重要意义。
机器学习中的数学基础涵盖了线性代数、概率论与统计学、微积分与优化以及信息论与编码等多个领域,这些数学工具不仅为机器学习算法的设计和实现提供了坚实的理论基础,还推动了人工智能技术的不断发展和创新,对于想要深入学习和实践机器学习的人来说,掌握这些数学基础是至关重要的。